Construyendo poliedros con sorbitos de colores.
Sexto año de arquitectura, generación 2011.
Construcción de poliedros regulares
Para construir poliedros con pajitas lo primero que necesitamos son, obviamente, pajitas. Conviene que estas no sean de las que tienen una parte flexible (o se debe quitar esa parte). También es conveniente que no sean demasiado frágiles para que no se nos rompan al tensar el hilo. Las pajitas podremos cortarlas en trozos más pequeños si no queremos que nos salga el poliedro demasiado grande. Pero lo que es importante es que los trozos que hagamos sean todos de la misma longitud.
También necesitaremos hilo de lana o alambre de bisutería. Este último es mejor porque se puede dirigir fácilmente por el interior de las pajitas y dará mayor rigidez al poliedro, lo que para el cubo o el dodecaedro será imprescindible pero no para los poliedros de caras triangulares.
En el caso de que usemos hilo, necesitaremos también una aguja para poder pasar el hilo por dentro de la pajita. Esta aguja tiene que ser más larga que los trozos de pajita que vayamos a usar. Si no tenemos una aguja así la podemos fabricar con un trozo de alambre en el que le hagamos un arito en un extremo para enhebrar en él el hilo.
CONSTRUCCIÓN DE UN TETRAEDRO
Este es el poliedro más fácil de construir y para ello necesitaremos 6 trocitos de pajita.
Primero vamos a construir un triángulo. Para ello pasa el hilo por tres trozos de pajita y átalos tensando lo más posible.
Antes de seguir construyendo, fíjate en que, si has tensado bien, el triángulo que obtienes es indeformable. Esta es una propiedad que el único polígono que la cumple es precisamente el triángulo. Todos los demás polígonos construidos así (cuadrados, pentágonos,...) se pueden mover, cambiando los ángulos. Precisamente por esta propiedad que ya conocían los antiguos griegos, construían los templos con un triángulo para sujetar el techo y hoy en día muchas estructuras se acaban uniendo formando triángulos para darles mayor rigidez. Esta propiedad nos va a permitir también que cuando construyamos los poliedros con caras triangulares (tetraedro, octaedro y dodecaedro), estos se mantengan rígidos aunque los hayamos hecho con hilo en lugar de alambre.
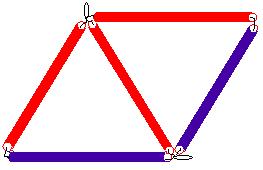
El siguiente paso en nuestra construcción será hacer otro triángulo adosado al anterior. Para ello pasa el hilo por una nueva pajita, luego por la de uno de los lados del triángulo que ya tenías construido y, por último por otra pajita nueva. Hecho esto haz un nudo en el hilo tesándolo para que quede el nuevo triángulo rígido.
Ya sólo nos queda terminar el vértice del tetraedro, que esta formado por tres caras triangulares. Para ello tienes que tomar un nuevo trozo de pajita, pasar por él el hilo y luego, sucesivamente, por cada uno de los lados de cada uno de los dos triángulos que vas a unir (por ejemplo, los azules del dibujo). Para poder hacerlo tendrán que levantar los dos triángulos por uno de los vértices comunes, para poder formar el vértice del tetraedro.
CONSTRUCCIÓN DE UN OCTAEDRO
El proceso de construcción del octaedro es muy parecido al del tetraedro. La única diferencia en que mientras en los tetraedros confluyen en un vértice tres triángulos, en el octaedro son cuatro. En este caso vas a necesitar 12 trocitos de pajita.
Comenzaremos de nuevo haciendo un triángulo y adosando a continuación otros dos como ves en la figura.
Ahora tenemos que cerrar el vértice con un cuarto triángulo. Para ello tienes que tomar un nuevo trozo de pajita, pasar por él el hilo y luego, sucesivamente, por cada uno de los lados de cada uno de los dos triángulos que vas a unir (los azules del dibujo), y al igual que hiciste en el tetraedro, tendrás que levantar los tres triángulos por el vértice común para que pueda cerrar.
Como verás, te habrá quedado una pirámide de base cuadrada. Para completar el octaedro bastará con formar otra pirámide por el otro lado, aprovechando la base cuadrada ya construida.
CONSTRUCCIÓN DE UN ICOSAEDRO
Si ya has construido los dos poliedros anteriores, construir el icosaedro es similar pero un poco más largo. Comienzas construyendo cuatro triángulos consecutivos al igual que hiciste dos y tres en las anteriores.
Y como viene siendo habitual, se trata ahora de cerrar el vértice con otro triángulo, porque en los vértices de los icosaedros confluyen cinco triángulos.
Con esto has construido una pirámide pentagonal. Pero ahora no basta con completar una pirámide igual por el otro lado. Vamos a seguir una estrategia distinta, que podíamos haber usado en las construcciones anteriores: ir completando vértices. Vamos a ver en qué consiste. Hemos dicho que en los vértices de un icosaedro confluyen 5 triángulos (en los del octaedro 4 y en los del tetraedro 3). Pues lo que hay que hacer es ir observando en cada vértice que nos vaya saliendo cuántos triángulos convergen e ir completando hasta que converjan 5.
En lo que habíamos construido hasta ahora, hay un vértice completo y otros cinco vértices donde sólo hay dos triángulos. Elegimos uno de ellos y lo completamos con otros tres triángulos. Una vez terminado esto veremos que aparte de dos vértices completos de 5 triángulos tenemos uno en el que confluyen tres, pues lo cerramos con otros dos, pero fíjate que para cerrar puedes ir aprovechado lo que ya tienes.
Este es el proceso que tienes que ir siguiendo. Vas mirando cuantos triángulos (también puedes contar pajitas que es lo mismo) convergen en cada vértice y los vas completando hasta 5 aprovechando lo que ya tienes. Así, poco a poco, llegará un momento que con añadir una última pajita habrás completado un icosaedro.
jueves, 28 de abril de 2011
SUCESIONES REALES
Informalmente, una sucesión de números reales es un conjunto ordenado de infinitos números reales a1, a2, a3, a4, a5,..., an,... Cada uno de los números reales se llama término de la sucesión.
De forma más rigurosa, una sucesión de números reales es una función cuyo dominio es el conjunto de los números naturales y codominio el conjunto de los números reales.
El conjunto ordenado de números impares 1, 3, 5, 7, 9, 11, 13,... es una sucesión de números reales. El término general puede escribirse así: an=2.n-1
Sin embargo, no todas las sucesiones tienen término general. Por ejemplo, en la sucesión de los números primos: 2, 3, 5, 7, 11, 13, 17, 19, 23,... no hay ninguna fórmula que exprese el término general.
En esta primer etapa de su estudio, nos proponemos los siguientes objetivos:
De forma más rigurosa, una sucesión de números reales es una función cuyo dominio es el conjunto de los números naturales y codominio el conjunto de los números reales.
El conjunto ordenado de números impares 1, 3, 5, 7, 9, 11, 13,... es una sucesión de números reales. El término general puede escribirse así: an=2.n-1
Sin embargo, no todas las sucesiones tienen término general. Por ejemplo, en la sucesión de los números primos: 2, 3, 5, 7, 11, 13, 17, 19, 23,... no hay ninguna fórmula que exprese el término general.
En esta primer etapa de su estudio, nos proponemos los siguientes objetivos:
- Encontrar regularidades en secuencias numéricas y geométricas.
- Encontrar el término general de una sucesión.
sábado, 9 de abril de 2011
PRIMER ESCRITO - MATEMÁTICA I -
Encontré este material que me pareció bueno para repasar intervalos e inecuaciones. Tiene muchos ejercicios que podrían hacer.
La propuesta:
escrito1FM1
Suscribirse a:
Comentarios (Atom)